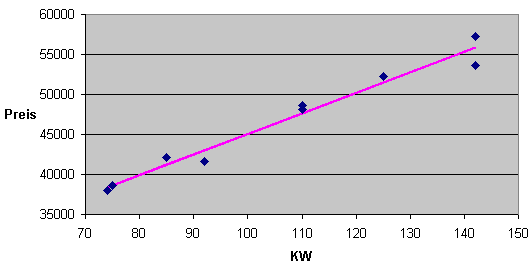
Trägt man den Preis über die KW graphisch auf, so ergibt sich folgendes Bild:
zurück zum Glossar (Kleinste Quadrate Methode)
Kleinste Quadrate Methode am Beispiel der linearen Regression.
Allgemeine Methode, aus Originaldaten die Parameter für ein zugrunde gelegtes theoretisches Modell zu berechnen.
Wenn die Originaldaten mit einem "zufälligen (also normalverteilten) Rauschen" behaftet sind ( "Messunschärfe" -> ALM), dann liefert die Minimierung der Summe der Abstandsquadrate (=kleinste Quadrate Methode) den besten Schätzwert für die Modellparameter.
Anders formuliert:
Die minimale Abstandsquadratesumme ist die Varianz der zugrundegelegten "Rausch-Normalverteilung".
Die kleinste Quadrate Methode wird durch den Satz von Gauss-Markov begründet und findet in der (multiplen) linearen Regression Anwendung.
Anhand der (univariaten) linearen Regression sollen die Grundzüge der Kleinsten Quadrate Methode dargelegt werden.
(Der allgemeinere Fall wird in Multipler Linearer Regression skizziert. Dort wird auch auf die Matrixschreibweise kurz eingegangen).
Die univariate Regression (also Regression mit genau einer unabhängigen Variablen) ist zwar der einfachste, aber immerhin häufigste Fall von Regression.
Das folgende univariate Beispiel soll die Rechen- und Gedankengänge der Regression mittels der Methode der Kleinsten Quadrate Schritt für Schritt einmal ausführlich aufzeigen.
Das selbe Beispiel findet man mit den entsprechenden Rechenformeln und zahlenmässigen Ergebnissen in der Exceldatei Regression.xls.
Eine Regressionsrechnung mit dem Excel Analysis Toolpak befindet sich ebenfalls in der Datei Regression.xls.
In dieser Exceldatei wird auch kurz auf quadratische Regression mit dem Analyse Toolpak eingegangen.
0.Einführung, Ausgangsdaten. [zu 1. hoch]
| Marke | KW | Preis |
Trägt man den Preis über die KW graphisch auf, so ergibt sich folgendes Bild:
|
| Audi | 74 | 38000 | |
| Audi | 92 | 41600 | |
| Audi | 110 | 48100 | |
| Audi | 142 | 53600 | |
| BMW | 75 | 38600 | |
| BMW | 85 | 42100 | |
| BMW | 110 | 48600 | |
| BMW | 125 | 52200 | |
| BMW | 142 | 57200 |
In das Bild bereits eingezeichnet ist eine Modellgerade, die die wirklichen Werte mehr oder weiniger gut annähert.
Die Modellgerade hat den Sinn,
Ziel der Regressionsrechnung ist es nun, die optimale Gerade herauszufinden. Das mathematische Kriterium hierfür ist, dass die Summe der Abstandsquadrate (genauer gesagt die Summe der Quadrate der senkrechten Lote der Punkte auf die Gerade) minimal wird.
1. Bestimmung der optimalen Modellparameter a und b. [zu 2. zu 0. hoch]
Gegeben sei eine "Punktewolke", die durch eine Gerade der Form
|
|
a,b: zu ermittelnde Modellparameter. |
angenähert werden soll.
Anmerkung: Dies macht natürlich nur dann Sinn, wenn ein linearer Zusammenhang zwischen x und y bereits "per Auge" naheliegt oder zumindest vermutet werden kann.
Rein rechnerisch kann man dies für die wildesten Punktewolken durchführen.
Es gibt jedoch Kenngrössen, die die "Modellgüte" charakterisieren (folgt weiter unten).
Natürlich wird die Gerade in den seltensten Fällen alle Messpunkte genau treffen. Vielmehr werden die Messpunkte einen mehr oder weniger grossen Abstand zur Geraden haben. Die einzelnen Abstände sind die jeweiligen Fehler des Modells.
Die Fehler werden als unabhängig normalverteilt angenommen.
Die exakten Verhältnisse kann man so beschreiben:
|
yi,schätz: Der durch die Gerade geschätzte
i-te Messwert der abhängigen Variablen, a,b: zu ermittelnde Modellparameter (hier: Steigung und Achsenabschnitt) fehleri: Abstand (in y-Richtung) des wahren i-ten Messwertes zum durch die Gerade geschätzten Wert. |
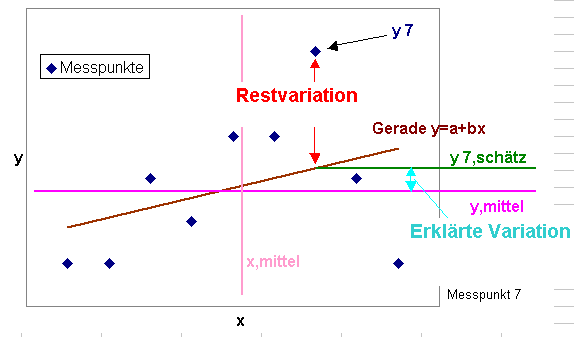
Folgende Skizze verdeutlicht die Zusammenhänge beispielhaft für einen Messwert Nr. 7:
| y7:
Messwert an der Messstelle x 7
fehler 7: Abstand des Messpunktes 7 von der Modellgeraden y 7,schätz: Der durch die Modellgerade angenäherte Wert von y 7 ymittel: Mittelwert aller durch das Modell genäherten Messwerte. xmittel: Mittelwert aller Messstellen |
Ziel ist es jetzt, die Gerade so zu legen, dass die Fehler möglichst klein werden.
Das Prinzip der kleinsten Quadrate besteht nun darin, die Summe aller quadrierten Fehler möglichst klein zu halten, also die Fehlerquadratesumme
zu minimieren. Mit der Geradengleichung
eingesetzt
ergibt dies:
Minimieren bedeutet partiell jeweils nach a und b ableiten, Nullsetzen, und nach a bzw. b auflösen.
(Auf den Nachweis: 2. Ableitung >0 wird verzichtet).
Man erhält somit als Schätzwerte für a und b:
und |
n: Anzahl Messwerte |
Der
Steigungsparameter b lässt sich auch darstellen als 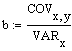
|
Da die Fehlerterme fehleri als unabhängig normalverteilt angenommen worden sind, sind die Modellparameter a und b ebenfalls unabhängig normalverteilt.
Die so bestimmten Modellparameter a und b sind reine Punktschätzungen, sagen also nichts über Vertrauensintervalle aus.
Meisstens interessiert jedoch insbesondere der Vertrauensbereich der Steigung. Könnte diese beispielsweise mit einer nicht zu vernachlässigenden Wahrscheinlichkeit genauso gut = Null sein, dann wäre y gar nicht von x abhängig und das gesamte Regressionsmodell somit fragwürdig.
Die Berechnung der Vertrauensintervalle folgt erst im übernächsten Abschnitt.
Zunächst soll die Qualität des gesamten Regressionsmodells , die "Modellgüte", berechnet werden.
2.Bestimmung der Modellgüte. [zu 3. zu 1. hoch]
Das bekannteste Mass für die Modellgüte ist das Bestimmtheitsmass B.
Es sagt etwas darüber aus, wie gut das Regressionsmodell im Ganzen ist, ohne direkte Aussagen über die einzelnen Modellparameter zu machen.
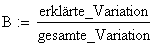 B ist das Quadrat des
Korrelationskoeffizienten.
B ist das Quadrat des
Korrelationskoeffizienten.
Unter "aufgeklärter Varianz" versteht man denjenigen Anteil der Quadratesummen, der durch die Hinzunahme der Regressionsgerade wegfällt. Dieser Anteil wird durch die Methode der kleinsten Quadrate ja maximiert
(die verbleibende Quadratesumme, Residuenquadratesumme bzw. Fehlerquadratesumme genannt, minimiert).
Folgendes Bild veranschaulicht noch einmal die Variationsanteile:
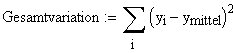
|
 |
| Anmerkung
1: Unter "Variationen" werden Quadratesummen verstanden.
Varianzen erhält man, indem man die Variationen durch die Anzahl
Freiheitsgrade, n dividiert. Da n hier überall gleich ist,
braucht zwischen Variation und Varianz nicht besonders unterschieden zu
werden.
Anmerkung 2: Gesamtvariation = Erklärte Variation + Restvariation |
|
Das Bestimmtheitsmass lässt sich einem Signifikanztestest unterziehen.
Es leuchtet intuitiv ein, dass das Bestimmtheitsmass rein zufällig umso grösser werden kann, je weniger Datenpunkte durch die Regressionsgerade genähert werden müssen.
Da
das Bestimmtheitsmass ![]() ein Quotient aus 2 Quadratesummen ist, kommt als
Test der
F-test
in Betracht. Allerdings enthält hier der Nenner den Zähler. Der F-Test
erfordert aber 2 voneinander unabhängige Variationen, etwa:
ein Quotient aus 2 Quadratesummen ist, kommt als
Test der
F-test
in Betracht. Allerdings enthält hier der Nenner den Zähler. Der F-Test
erfordert aber 2 voneinander unabhängige Variationen, etwa: ![]() .
.
Mit
B
eingesetzt ergibt sich ![]() .
.
Mit der Excelfunktion FVERT(F,1,n-2) ergibt sich schliesslich die (hoffentlich sehr kleine) Wahrscheinlichkeit p (Alpha Risiko), mit der die Originaldaten nur rein zufällig sich durch die Regressionsgerade derart gut beschreiben lassen würden
(in Wahrheit y von x gar nicht abhinge).
1-p ist das Signifikanzniveau für B.
3. Bestimmung der Vertrauensintervalle der Modellparameter a und b. [zu 4. zu 2. hoch]
Da die Fehlerterme ursprünglich als unabhängig normalverteilt angenommen worden sind, sind die Modellparameter ebenfalls (asymptotisch) normalverteilt. Zur Berechnung der Vertrauensintervalle von a und b benötigt man also die Varianz oder die Standardabweichung (Hier auch Standardfehler genannt), der Residuen.
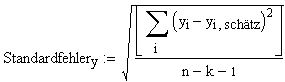
n: Anzahl Datenpunkte, k: Anzahl erklärender Variablen (hier: =1;"x"). Im Nenner steht also (n-2).
Die "Unschärfe" der durch das Modell geschätzten Werte der abhängigen Variablen y bewirkt also eine "Unschärfe" der Modellparameter a und b.
Unter Verzicht auf weitere Herleitungen (Ausführliche Herleitung befindet sich in Multiple lineare Regression) ergeben sich die Standardfehler (hier:=Standardabweichungen) der Modellparameter a und b zu:
| Standardfehler des Offsets a | Standardfehler der Steigung b |
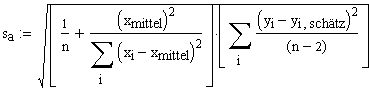 |
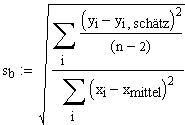 |
|
Anmerkung: Dies ist das Quadrat des Standardfehlers des y-Schätzwertes an der Stelle x=0. Das Quadrat des Standardfehlers des y-Schätzwertes an beliebigen Stellen x siehe unten. |
Anmerkung:
Diese Formel kann man sich intuitiv wie folgt verdeutlichen: Der Standardfehler einer Steigung muss sich zusammensetzen aus einem Quotienten ("Steigungsdreieck") zwischen Standardfehler y und Standardfehler x Im Nenner fehlt hierzu lediglich der Faktor 1/(n-1). Dies liegt daran, dass das sb bereits so hingetrimmt ist, dass die Formel für das Konfidenzintervall einfacher wird (Siehe Anmerkung weiter unten). |
| Mit der Umformung |
|
| |
|
Die Modellparameter sind bekanntlich normalverteilt. Dies gilt aber nur für "grosse" Anzahlen Datenpunkte.
(-> asymptotisch normalverteilt). Für "kleine" Anzahlen Datenpunkte sind die Modellparameter jedoch t-verteilt mit n-2 Freiheitsgraden:
Die zweiseitigen Vertrauensintervalle zum gegebenen Alpha Risiko lauten also:
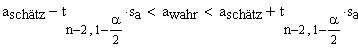 |
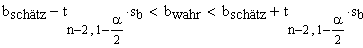 |
Der
Schwellenwert
![]() kann
durch
die Excelformel
TINV(a,n-2) berechnet werden.
kann
durch
die Excelformel
TINV(a,n-2) berechnet werden.
| Normalerweise lauten Formeln mit
Vertrauensintervallen mit der t-Verteilung beispielsweise wie rechts
stehend.
Im Zähler steht eine Standardabweichung und im Nenner Wurzel(n). Das Wurzel(n) ist in das sa bereits hineingerechnet worden, da sa (n bedeutet hier die Anzahl Freiheitsgrade). |
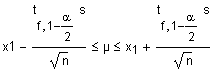 |
4. Berechnung der Vertrauensintervalle eines einzelnen ursprünglichen Messwertes.
Der Standardfehler eines bereits vorliegenden y-Wertes an der Stelle xk beträgt (ohne weitere Herleitung)
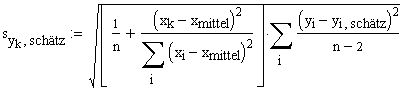
Das zweiseitige Vertrauensintervall zum gegebenen Alpha Risiko lautet demnach:
![]()
Der
Schwellenwert
![]() kann
durch
die Excelformel
TINV(a,n-2) berechnet werden.
kann
durch
die Excelformel
TINV(a,n-2) berechnet werden.
5. Bestimmung der Vertrauensintervalle prognostizierter Werte. [zu 6. zu 4. hoch]
(Werte, die nicht zu den ursprünglichen Messwerteni gehören)
Der Standardfehler für einen prognostizierten Wert beträgt (ohne weitere Herleitung):
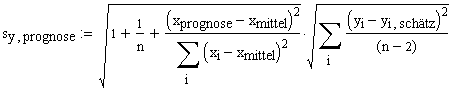
Demnach lautet das zweiseitige Vertrauensintervall zum gegebenen Alpha Risiko
![]()
6. Bestimmung des Vertrauensintervalles des gesamten Modells [zu 5. hoch]
Hier geht es um den Vertrauensbereich des gesamten Modells.
Dies ist das Vertrauensintervall für die Geradengleichung, die Einhüllende der Schar von Geraden, die in das Vertrauensintervall fallen.. Dieses ist kleiner als alle einzelnen Vertrauensintervalle der Schätzwerte, da ja die gesamte Gerade auf einmal betrachtet wird.
Das folgend angegebene Vertrauensintervall ist als Gleichung für alle Punkte zusammen zu sehen und sagt nichts über die Vertrauensintervalle der einzelnen Werte aus.
Es wurden 2 Modellparameter bestim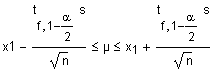 mt, a und b.
mt, a und b.
Im Gegensatz zu den vorangehend berechneten Vertrauensintervallen kommt nicht mehr die t-Verteilung, sondern die F-Verteilung zum Einsatz.
Es werden 2 Mittlere Quadratesummen miteinander verglichen, die mittlere Regressionsquadratesumme mit 2 Freiheitsgraden und die mittlere Residuenquadratesumme mit n-2 Freiheitsgraden. Erstere ist idealerweise möglichst gross, letztere idealerweise möglichst klein.
Das zweiseitige Vertrauensintervall zum gegebenen Alpha Risiko beträgt ohne weitere Herleitung
![]()
26.08.2005
zurück zum Glossar (Kleinste Quadrate Methode)