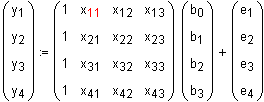
zurück zum Glossar (multiple lineare Regression)
Multiple Lineare Regression
Zunächst wird die Matrixschreibweise anhand eines Beispiels mit 3 unabhängigen Variablen (x1, x2, x3) vorgestellt, anschliessend ein Beispiel mit einer unabhängigen Variablen Schritt für Schritt inclusive Vertrauensintervalle durchgerechnet.
Das Gleichungssystem für das Beispiel multiple lineare Regression mit 3 unabhängigen Variablen und 4 Messungen sieht wie folgt aus:
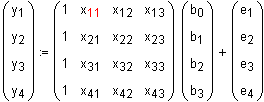
Hier bedeutet z.B. y3 den dritten Messwert der einzigen abhängigen
Variablen y, und z.B. x42 den 4. Messwert der unabhängigen Variablen x2.
Die ersten beiden von 4 Gleichungen lauten demnach
![]()
Obige Matrixgleichung kann man in Matrixnotation wie folgt einfacher darstellen:
Multiple Lineare Regression:
Berechnung der Modellparameter bj mittels Kleinster Quadrate Methode.
Die Fehler-Quadratesumme im Falle der einfachen linearen Regression lautet anschaulich
, mit der
Geradengleichung
eingesetzt ergibt dies
QSFehler ist lediglich eine andere Bezeichnung für Summe (ei2) und ist hier nichts Anderes als e12+e22+e32+e42.
Der Index i kennzeichnet die Nummer der Messung.
Die
letzte Gleichung etwas umgeschrieben lautet
In
Matrixschreibweise sieht das wie folgt aus:
.
X ist eine Matrix, e, y und b sind Vektoren. Der Index T bedeutet "Zeilen und Spalten vertauscht".
Das Entscheidende hieran ist, dass diese Gleichung für lineare Regressionsmodelle mit beliebig vielen unabhängigen Variablen gilt.
Mit den "speziellen" Rechenregeln der Matrixschreibweise lassen sich die zu entwickelden Ergebnisse relativ einfach erreichen, ohne sich mit dem schier unüberschaubaren Trümmerhaufen an Gleichungen der konventionellen Schreibweise herumzuschlagen.
Letzte
Gleichung ausmultipliziert ergibt
.
Ziel ist die Minimierung der Quadratesumme eTe (=QSFehler). Deshalb muss man nach b ableiten und Nullsetzen.
= 0
<=>
Multiplikation beider Seiten mit (XT X)-1 ergibt schliesslich
Auf den Nachweis dass die 2. Ableitung <0 ist, sei hier verzichtet.
XTX sieht ausgeschrieben wie folgt aus:
Rechenvorschrift, Beispiel:
(XTX)-1 zu berechnen ist etwas aufwendiger.
In der höheren Trickkiste der Matrixalgebra findet man folgende Beziehung:
Hierbei ist Det(A) die Determinante von A,
(Aij) ist eine Matrix mit ebensovielen Zeilen und Spalten wie A.
Aij sind die sogenannten Adjunkten von A.
Die Adjunkte Aij ist die mit (-1)(i+j) multiplizierte Determinante der um die i-te Zeile und j-te Spalte beraubten Matrix A.
Dies für das obige Beispiel in ausgeschriebener Form darzustellen würde jeglichen Rahmen völlig sprengen.
In der Praxis wird man deshalb um spezielle Statistiksoftware nicht herumkommen.
Spätestens jetzt sollte der Berechtigungsgrund der vereinfachten Matrixschreibweise mit all ihren "besonderen" Rechenregeln offenbar werden.
Danach wird XT mit dem Vektor y multipliziert (jede Zeile der Matrix wird mit der Spalte des Vektors y multipliziert. Es resultiert ein Vektor)
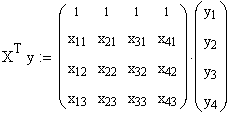 ,
ausmultipliziert:
,
ausmultipliziert: 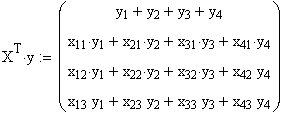
und das Ergebnis (->Vektor) dann schliesslich mit (XTX)-1 multipliziert (-> Vektor b).
Multiple Lineare Regression
Berechnung der Vertrauensintervalle der Modellparameter bj.
Die Varianz-Kovarianzmatrix der Parameter bj berechnet sich wie folgt.
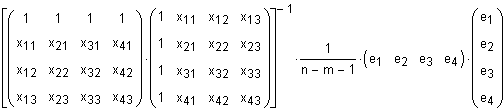
n: Anzahl Realisierungen, Messungen (hier: 4)
m: Anzahl unabhängiger Variablen (hier: 4; b0.....b3)
Der Bruch 1/(n-m-1) ist die Anzahl Freiheitsgrade.
Die Varianz-Kovarianzmatrix, dargestellt mit den bj, führt nach einigen Rechenschritten schliesslich zu folgender Gestalt:
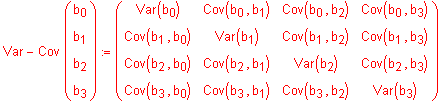
Var(b0) bedeutet beispielsweise die Varianz des Parameters b0, resultierend aus der Varianz der Residuen ei.
Cov(b0,b1) bedeutet die gemeinsame Kovarianz der beiden Parameter b0 und b1.
Die Varianz-Kovarianzmatrix zeigt die gesamte Streuung der Parameter bj untereinander.
Für die anschliessende Berechnung der Vertrauensintervalle bedeutet das, dass die Vertrauensintervalle der Parameter bj zusammenhängen, aufgrund der Kovarianzen also nicht unabhängig voneinander sind.
Vorstellen kann man sich das im zweidimensionalen Fall (1 unabhängige Variable, 2 Parameter: b0 und b1) als Vertrauensellipse, im dreidimensionalen Fall (2 unabhängige Variable, 3 Parameter: b0, b1 und b2) als Vertrauensellipsoid.
Natürlich lassen sich auch isolierte Vertrauensintervalle für einzelne Parameter bj berechnen.
Allerdings hat man dann keinerlei Aussage über die Vertrauensintervalle der restlichen Parameter bj.
"Überlagert" man die einzeln berechneten Vertrauensintervalle der bj, dann erhält man im zweidimensionalen Fall ein Vertrauensrechteck, im dreidimensionalen Fall einen Vertrauensquader.
Das Vertrauensrechteck umfasst die "richtig" berechnete Vertrauensellipse und berührt sie an 4 Stellen.
Hier wird deutlich, dass die "Überlagerung" der getrennt berechneten Vertrauensintervalle zu grosse Vertrauensintervalle liefert (konservativ).
Entsprechendes gilt für den dreidimensionalen Fall sowie höherdimensionale Fälle.
Die Ausgangsgleichung
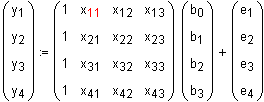
kann man auch wie folgt darstellen:
y,b und e sind Vektoren, X eine Matrix.
Entsprechend lässt sich die Varianz-Kovarianzmatrix
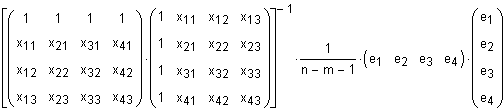
auch wie folgt darstellen:
eT ist der transponierte Vektor von e (Zeilen und Spalten vertauscht.)
eTe sieht ausgeschrieben so aus: (e1)2+(e2)2+(e3)2+(e4)2 , also die Quadratesumme der Residuen.
XT ist die transponierte Matrix von X (Zeilen und Spalten vertauscht.)
(XTX)-1 ist die inverse Matrix zu XTX.
Wie XTX ausgeschrieben aussieht, wurde weiter oben bereits dargestellt.
Dort ist auch beschrieben, wie man (XTX)-1 berechnet.
Bleiben wir also bei der vereinfachten Matrixdarstellung der Varianz-Kovarianzmatrix
Die Varianz-Kovarianzmatrix beihaltet die gemeinsamen Streuungen der Parameter bj.
Diese Streuungen haben ihre Ursache in der Streuung der (normalverteilten) Residuen und sind somit ebenfalls normalverteilt.
Da aber die Streuungen aus den Daten berechnet werden und nicht von vorne herein bekannt sind, sind die Streuungen t-verteilt.
Nun handelt es sich aber um zusammenhängende Streuungen der Parameter bj, das heisst, sie streuen "gemeinsam".
Diese gemeinsame Streuung der bj ist Hotelling T2 verteilt.
Die Hotelling T2 Verteilung kann hier zwar nicht mathematisch hergeleitet werden; ein Analogieschluss von der (eindimensionalen) t-Verteilung wird den Sachverhalt jedoch verdeutlichen:
Die Prüfgrösse t bei eindimensionalem Datenmaterial lautet bekanntlich:
Hier liegt die Nullhypothese zugrunde, dass der aus der Stichprobe ermittelte Mittelwert xquer gleich dem "wahren" (aber unbekannten) Mittelwert µ ist.
µ wird in den meissten Fällen der (multiplen) linearen Regression =0 gesetzt, das heisst, man testet, ob die Parameter des Regressionsmodells signifikant von Null verschieden sind (das Modell also überhaupt seine Berechtigung hat).
In obiger Formel ist
(ohne Indizes)
die "fertig" berechnete Streuung des Parameters bj, und s die Streuung der Ausgangswerte.
Das Wurzel n kommt vom zentralen Grenzwertsatz.
Dieser Ansatz (für jeden Parameter bj ein getrenntes Vertrauensintervall) wird aber der Gemeinsamkeit der Streuungen der bj untereinander nicht gerecht und führt, wie zuvor bereits erwähnt, zu konservativen Resultaten (zu grosses gemeinsames Vertrauensintervall, im zweidimensionalen Fall Rechteck statt Ellipse)
Bezug zur Hotelling T2 Verteilung:
Quadriert man
, so ergibt sich mit etwas Umformung
.
Für den mehrdimensionalen Fall erhält man analog Hotelling's T2:
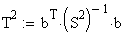
Hier ist S2 eine "verallgemeinerte" Varianz: Die Varianz-Kovarianzmatrix.
Für die Berechnung der inversen Matrix von S2 gilt wieder die weiter oben genannte allgemeine Beziehung für Matrizen:
Nun sind die Schwellenwerte zu T2 zwar nicht tabelliert.
Es gibt aber eine "angenehme" Beziehung zur F-Verteilung:
Somit repräsentieren die Lösungen der Gleichung
das gemeinsame Vertrauensintervall der Parameter bj.
Diese Gleichung ist von der Ordnung j und enthält sämtliche gemischten Glieder.
Im vierdimensionalen Fall (3 unabhängige Variablen -> 4 Parameter b0,b1,b2,b3) also b02, b0b1, b0b2, b0b3, b12, b1b2, b1b3, b22, b2b3 und b32.
Beispiel
Im Folgenden werden die optimalen Parameter sowie die Vertrauensintervalle einer linearen Einfachregression allgemein (also ohne konkrete Zahlen) Schritt für Schritt durchgerechnet.
Dieses Beispiel ist für das anschauliche Verstehen hinreichend einfach, jedoch bereits umfassend genug für die Abhandlung in Matrixschreibweise.
Ein weiterer Vorteil gerade des linearen Einfachregressions-Beispiels ist, dass sich alle wesentlichen Endergebnisse auch ohne Matrixschreibweise noch halbwegs übersichtlich darstellen lassen, womit ein Bezug zu der an anderer Stelle auf "herkömmliche" Weise berechneten linearen Einfachregression hergestellt werden kann.
Leider jedoch sind die Rechnungen sehr umfangreich.
Gegeben seien 4 Wertepaare (x|y), für die eine einfache lineare Regression mit Vertrauensintervallen der beiden Modellparameter (Steigung b1 und Achsenabschnitt b0) durchgeführt werden soll.
Bestimmung der optimalen Parameter b0 und b1.
Die
allgemeine Modellgleichung
bekommt hier die
Gestalt
|
|
Da lediglich eine unabhängige Variable (x) vorkommt, kann der zweite Index entfallen. x1 bedeutet dann lediglich den Wert, den x bei der ersten Messung inne hatte. e1...e4 sind die Fehler, die trotz des zu entwickelnden Modells (Geradengleichung) noch übrig bleiben. |
Die erste der 4 Gleichungen lauten also:
y1 = 1*b0 + x1*b1
+ e1
Der Vektor b des "optimalen" (mit der kleinsten Quadrate Methode bestimmten) Modells berechnet sich zu
Ausgeschrieben sieht das in diesem Beispiel wie folgt aus:
Zunächst
bestimmen wir XTX. Ausmultipliziert ergibt sich folgende
Gestalt:
Zur Bestimmung der inversen (XTX)-1 benötigt man folgenden, bereits weiter oben beschriebenen Trick.
Hierbei ist Det(A) die Determinante von A,
(Aij) ist eine Matrix mit ebensovielen Zeilen und Spalten wie A.
Aij sind die sogenannten Adjunkten von A.
Die Adjunkte Aij ist die mit (-1)(i+j) multiplizierte Determinante der um die i-te Zeile und j-te Spalte beraubten Matrix A.
Die Determinante von XTX lautet
Das
kann man wiederum schreiben als: ,
bzw.
mit n=4 und xquer: Mittelwert(xi)
Letztere
Formel ist wiederum nichts Anderes als
(Verschiebungssatz)
Zur Bestimmung des linken oberen Elementes der inversen Matrix streicht man also diejenige Zeile und Spalte, die zu dem linken oberen Element (1+1+1+1) gehören.
Es bleibt dan in diesem Beispiel lediglich das rechte untere Element übrig (x12+x22+x32+x42).
Davon die Determinante, multipliziert mit (-1)(1+1) ergibt das Element selbst. (Die Determinante einer 1x1 Matrix, also einer einfachen Zahl ergibt die Zahl selbst).
Insgesamt erhält man so für (XTX)-1
Dies
wird nun mit
multipliziert,
und man erhält folgende Form:
=
Schreibt man den rechten Teil dieses Terms in allgemeiner Form (also n anstatt 4 Mesungen), so ergibt sich für b schliesslich allgemein:
=
Dies ist ein Ausdruck, der 2 Gleichungen enthält: Eine für b0 und eine für b1.
Im Folgenden sollen diese beiden Gleichungen vereinfacht werden.
Zunächst b1:
|
.............................................................. (1) |
Das zweite Glied in der Klammer von (1) kann man sich als einen Teil des Ausdrucks
Das geht wie folgt: Multipliziert man den Ausdruck (3) aus, so erhält man: Man erhält: bzw. |
Setzt man (2) in (1) ein, so ergibt sich
|
................................................................................. |
Man mache sich klar, dass die beiden vorkommenden Doppelsummen, also der erste Term nach der ersten öffnenden Klammer und der letzte Term vor den beiden schliessenden Klammern, gleich sind (und sich somit wegheben). n*xquer ist nämlich dasselbe wie S(xi), da der Index i von 1 bis n läuft.
|
Schliesslich erhält man für b1
,
was mit dem unter konventioneller Berechnung erhaltenen Ergebnis
(-->
Kleinste
Quadrate Methode) übereinstimmt.
Nun zu b0:
|
................................................................. |
Für einen Teil dieser Formel gelten die selben Umformungsschritte wie bei der Herleitung von b1. |
Es ergibt sich:
(ganz
rechts fehlt eine 2. schliessende Klammer) |
Der Vorfaktor-Term (ganz links) und der Term nach der 2. öffnenden Klammer ergeben genau b1. Ferner ist S(xi) = n*xquer und S(yi) = n*yquer Letztgenanntes betrifft alle verbleibenden Terme. |
Man erhält:
|
|
Beachte:
|
Somit ergibt sich
|
|
Beachte: |
Schliesslich erhält man für b0
,
was mit dem unter konventioneller Berechnung erhaltenen Ergebnis
(-->
Kleinste
Quadrate Methode) übereinstimmt.
Bestimmung der Vertrauensintervalle von b0 und b1.
Die Varianz-Kovarianzmatrix berechnet sich allgemein zu
=
.
Weiter oben wurde XTX zu
berechnet,
und die Inverse Matrix (XTX)-1 zu
Anstelle des Termes 1/(n-m-1)*eTe, der ja nichts Anderes als die Varianz der Residuen ist, schreiben wir ab jetzt s2error.
Ferner schreiben wir anstelle der einzelnen Summanden mit Index von 1 bis 4 nun allgemeine Summenausdrücke.
Demnach ergibt sich die Varianz-Kovarianzmatrix zu
|
= S2 |
Hier kann man bereits Einiges ablesen:
Die Varianz von b0 für sich alleine
genommen ist die Varianz von b1 für sich alleine genommen ist
Die Kovarianz zwischen b0 und b1 ist
|
Die Varianz-Kovarianzmatrix ist, wie weiter oben bereits erwähnt, eine verallgemeinerte Varianz, die man auch als S2 bezeichnet.
Die Vertrauensintervalle von b0 und b1 ergeben sich nach der weiter oben angegebenen Formel zu
In diesem Beispiel ist j=2 (2 Parameter, b0 und b1) und n=4 (4 Messwerte). Für die weiteren Schritte lassen wir jedoch n allgemein.
a ist das Signifikanzniveau, bzw. diejenige Wahrscheinlichkeit, mit der die "wahren" (aber unbekannten) Parameter b0 und b1 innerhalb des zu berechnenden Vertrauensintervalles liegen. a ist typischerweise 90% oder grösser.
Berechnen wir zunächst (S2)-1.
Zur Erinnerung, wie man inverse Matrizen berechnet (weiter oben beschrieben):
Hierbei ist Det(A) die Determinante von A,
(Aij) ist eine Matrix mit ebensovielen Zeilen und Spalten wie A.
Aij sind die sogenannten Adjunkten von A.
Die Adjunkte Aij ist die mit (-1)(i+j) multiplizierte Determinante der um die i-te Zeile und j-te Spalte beraubten Matrix A.
Die Determinante von S2 lautet
|
|
Man mache sich klar, dass der Nenner des Vorfaktors (ohne das äussere Quadrat) und die erste Klammer im Zähler gleich sind. Es ist nämlich n*S(xi2) = n*n*(x2)quer und [S(xi)]2 = n*n *(xquer)2 Ferner ist |
Also ist 1/Det(S2)
(S2)-1 ergibt sich hiermit zu
=
Die Gleichung für die Vertrauensintervalle
lautete , mit j=2.
Ausgeschrieben hat das die Form:
Zuerst bT mit (S2)-1ausmultipliziert:
,
und schliesslich
|
|
mit
|
|
Dies ist eine quadratische Form aus 2 unabhängigen Variablen b0 und b1. Aus der linken Seite der Gleichung ergibt sich durch die Anzahl n der Messungen und dem festzulegenden a ein fester Zahlenwert. b0 und b1 sind nun so zu wählen, dass die Gleichung erfüllt ist. Die Lösungsmenge der b0 und b1 beschreibt eine Ellipse im zweidimensionalen Raum, aufgespannt durch b0 und b1. |
|
25.08.2005
zurück zum Glossar (multiple lineare Regression)