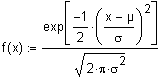
Gauss'sche Normalverteilung
Vorbemerkung:
Unter dem Begriff Normalverteilung, auch Gauss-Verteilung, wird landläufig die glockenförmige Kurve verstanden.
Formal korrekt handelt es sich bei der Glockenkurve aber um die (Wahrscheinlichkeits-) Dichtefunktion der Normalverteilung.
Die Normalverteilung selbst ist das Integral der Dichtefunktion, also eine S-förmige Kurve.
Dieser Sachverhalt gilt sinngemäss für alle Verteilungsfunktionen.
In dieser Rubrik wird ausnahmsweise die landläufig übliche Bezeichnung Normalverteilung für die Dichtefunktion verwendet.
Die Normalverteilung ist die wichtigste Verteilungsfunktion in der Statistik.
Begründungen folgen am Ende dieser Rubrik.
Die Normalverteilung besitzt 2 Parameter, µ ( Mittelwert) und s ( Standardabweichung).
Normalverteilung ist "Additives Rauschen":
Wirken unendlich viele kleine Einflüsse additiv auf eine Zufallsvariable ein, dann ist diese Variable normalverteilt.
(Siehe auch Fehlerfortpflanzungsgesetz)
Tests auf Normalverteilung sind unter Anderem (Testaufwand nimmt nach unten zu):
Die standardisierte Normalvetreilung besitzt den Mittelwert 0 und die Standardabweichung 1.
Die allgemeine (nicht standardisierte) Form der Dichtefunktion hat die Gestalt
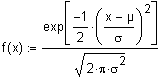
µ:
Erwartungswert, Mittelwert
s: Standardabweichung
Der Vorfaktor (2ps2)1/2 stellt sicher, dass der Flächeninhalt unter der Kurve (das Integral der Dichtefunktion, also die Verteilungsfunktion) den Wert 1 bekommt. Dies nennt man Normierung.
Wahrscheinlichkeiten können nämlich nicht grösser als 1 werden.
| Erwartungswert | Varianz | Schiefe | Wölbung | Modalwert | Median | Bemerkungen |
| µ | 0 | |
µ | µ |
F: Verteilungsfunktion: nicht geschlossen darstellbar.
Die Schiefe der Normalverteilung ist = 0, also die Normalverteilung ist symmetrisch.
Mittelwert, Modalwert und Median fallen demnach zusammen.
Die Wendepunkte liegen an den Stellen µ+s und µ-s.
Je grösser s, desto "breiter" oder "flacher" ist die Kurve.
Eine Exceldatei zum "Ausprobieren" verschiedener µ und s befindet sich hier unter Normalverteilung.xls.
Da die Verteilungsfunktion, also die kumulierte Normalverteilung, nicht geschlossen darstellbar ist, werden in vielen praktischen Fällen andere Verteilungsfunktionen herangezogen, die der Normalverteilung insofern "ähnlich sehen", als dass sie S-förmig sind (im Grunde ist jede Verteilungsfunktion S-förmig):
Fermiverteilung
Siehe z.B. Logit Modell.
Die Normalverteilung nimmt in der Statistik eine besonders herausragende Stellung unter den Verteilungsfunktionen ein, weshalb zahlreiche Tests entworfen wurden, um Datenmaterial auf Normalverteilungsform zu untersuchen. Siehe hierzu Anpassungstest.
Begründung:
Additives Rauschen, also der additive Einfluss vieler kleiner verschiedener Störungen auf eine Zufallsvariable machen diese Variable normalverteilt. Dies ist in der Theorie der Messfehler von grosser Bedeutung. (Multiplikatives Rauschen: -> Lognormalverteilung)
nahezu alle parametrischen Tests beruhen auf der Annahme normalverteilter Daten.
Einige andere Verteilungsformen gehen bei bestimmten
Grenzübergängen in die Normalverteilung über. Hier sind insbesondere
die Binomialverteilung und die Poissonverteilung
gemeint.
Siehe dazu
Die grösste Bedeutung der Normalverteilung in der Statistik tritt jedoch erst durch den
zentralen Grenzwertsatz zu Tage: Mittelwerte aus Stichproben sind approximativ normalverteilt, egal wie die Ausgangsverteilung aussieht (dies ist eine technische Formulierung; mathematisch gibt es ein paar [technisch unbedeutende] Einschränkungen.
Von der Normalverteilung abgeleitet sind folgende statistisch bedeutsame "Hilfsverteilungen":
Diese 3 Verteilungsfunktionen sind keine "natürlichen" Wahrscheinlichkeitsverteilungen, sondern technische Konstrukte, die bei statistischen Berechnungen (-> Vertrauensintervalle) äusserst hilfreich sind.
Für eine graphische Darstellung der Normalverteilung in Excel siehe hier.
Für eine Veranschaulichung der Beziehungen
Hypergeometrische Verteilung - Binomialverteilung - Poissonverteilung - Normalverteilung
Zur graphischen Berechnung von Vertrauensintervallen der Normalverteilung siehe Wilrich Nomogramm.
Zur graphischen Berechnung von Überschreitungsanteilen der Normalverteilung siehe Durrant Nomogramm.
Für eine zusammenhängende mathematische Darstellung der selben Beziehungen siehe hier.
Für die Bestimmung der "optimalen" Parameter s und µ einer normalverteilten Stichprobe siehe Beispiel unter Maximum Likelihood Estimation (MLE).
Siehe auch Tschebyscheff'sche Ungleichung.
Für die Erweiterung der Normalverteilung auf mehrere Dimensionen siehe mehrdimensionale Normalverteilung.
12.09.2005
Gründe für die Bedeutung der Normalverteilung
1. Obwohl Normalverteilung kumuliert nicht geschlossen darstellbar ist, hat sie dennoch gute mathematische Eigenschaften, die sie EDV-technisch handhabbar machen.
2. Normalverteilung beschreibt "Additives Rauschen": Unendlich viele voneinander unabhängige Einflüsse, additiv zusammengesetzt, ergeben exakt Normalverteilung.
--> Normalverteilung ist DIE Verteilung für Messunsicherheit. (siehe auch Fehlerfortpflanzungsgesetz)
Mittelwerte von Stichproben sind approximativ normalverteilt, EGAL wie die Verteilung der Einzelwerte aussieht (!)
Approximativ bedeutet, dass die Aussage umso besser stimmt, je grösser die Stichprobe ist.
Das muss man sich mal vorstellen:
Man zieht aus einer egal wie "unmöglich" aussehenden Verteilung wiederholt Stichproben und stellt fest, dass der Stichprobenmittelwert normalverteilt ist. Mathematisch gibt es diesbezüglich Einschränkungen, die jedoch kaum praxisrelevant sind.
4.
Das Prinzip Maximaler Entropie.
Der Kenntnisstand "Wir kennen Mittelwert, Standardabweichung und wissen sonst (auch technisch) nichts" wird am treffendsten durch die Normalverteilung beschrieben, das heisst,
Normalverteilung Annahme lässt hier die grösstmögliche Unsicherheit zurück, gaukelt nicht mehr Wissen vor als man hat, entspricht also genau zuvor genanntem Kenntnisstand.
Für den Kenntnisstand "Wir kennen nur den Mittelwert und wissen sonst (auch technisch) nichts" ist entsprechend die Exponentialverteilung die "richtige" Verteilungsfunktion.