Wichtige parametrische Verteilungsfunktion in der Statistik. Ein Parameter, genannt Freiheitsgrad .
Zieht man aus einer standardisierten Normalverteilung
(also Normalverteilung mit Mittelwert µ=0 und Standardabweichung s=1) n Werte,
teilt deren Mittelwert Xquer durch dessen Standardfehler, dann ist dieses Ergebnis t-verteilt mit (n-1) Freiheitsgraden..
.
Hier ist s die aus den n Werten berechnete Standardabweichung und Xquer der aus den n Werten berechnete Mittelwert.
Zur Erläuterung ein kleiner Exkurs:
Würde in zuvor genannter Formel anstelle s s stehen, (die Standardabweichung also bekannt [hier=1] sein, dann lautete die Formel (Mit Z anstelle t):
Z = Xquer*Wurzel(n).
Aufgrund des zentralen Grenzwertsatzes, wonach die Mittelwerte aus beliebigen Ausgangsverteilungen (also auch hier bei normalverteilter Ausgangsverteilung) normalverteilt sind, ist Z normalverteilt, und zwar mit einer gegenüber der Ausgangs(normal)-verteilung um Wurzel(n) gestauchten Skala.
Mit anderen Worten: Xquer*Wurzel(n) ist standardnormalverteilt, Xquer also normalverteilt mit einer um Wurzel(n) kleineren Standardabweichung als die Standardabweichung (hier=1)der Ausgangsverteilung.
Wir haben bisher die Standardabweichung ohne Beschränkung der Allgemeinheit festgelegt zu 1.
Alles bisher Gesagte entspricht dem praktischen Fall, wo die Standardabweichung der zugrundeliegenden Ausgangsverteilung BEKANNT ist (Ohne Beschränkung der Allgemeinheit: =1).
In den meisten praktischen Fällen ist die Standardabweichung jedoch NICHT BEKANNT, weshalb man sie aus der gezogenen Stichprobe schätzen muss. Diesem Sachverhalt trägt das s anstelle des s Rechnung.
Dies hat wiederum zur Folge, dass das t in obiger Formel nicht mehr normalverteilt ist, sondern eben t-verteilt.
Die Wurzel(n) trägt wie im zuvor geschilderten Fall der Normalverteilung der Tatsache Rechnung, dass s die Standardabweichung der Ausgangsdaten ist, und die Standardabweichung des Mittelwertes einer Stichprobe ja um den Faktor Wurzel(n) kleiner ist.
Wenn s der Grundgesamtheit genau = 1 sein sollte, dann werden die s der Stichproben um diesen Wert streuen. Genau aus diesem Grund ist die t-Verteilung breiter als die Normalverteilung.
Die t-Verteilung ist in der Mitte umso schmaler und hat umso breitere Schwänze, je kleiner n ist.
Für grosse n nimmt die t-Verteilung Normalverteilungsform an, da für grosse n die Stichprobenmittelwerte sehr nahe beim "wahren" Mittelwert der Normalverteilung liegen (=0) und die Standardabweichungen der Stichproben sehr nahe an der "wahren" Standardabweichung der Normalverteilung (=1) liegen.
Dies wird im Arbeitsblatt "Gamma_t" in folgender Exceltabelle bildlich dargestellt.
Alternativ kann man auch sagen, die t-Verteilung ist der Quotient aus einer normalverteilten Zufallvariablen und der Wurzel einer Chi Quadrat verteilten Zufallsvariablen.
(Beide
Zufallsvariablen unabhängig voneinander. Diese Annahme ist
nicht trivial und trifft nur für normalverteilte Daten zu).
Zusammenhang mit der F-Verteilung F(m,n):
Wenn man letzte Formel quadriert, dann steht im Nenner die Chi Quadrat Verteilung mit n Freiheitsgraden und im Zähler die quadrierte normalverteilte Zufallsvariable, was ja nichts Anderes ist als die Chi Quadrat Verteilung mit nur einem Freiheitsgrad.
Folglich ist das Quadrat der t-Verteilung gleich F(1,n)
Anwendungen: Vertrauensintervalle für Mittelwerte, statistische Tests für Mittelwerte und Mittelwertdifferenzen.
| Erwartungswert | Varianz | Schiefe | Wölbung | Modalwert | Median | Bemerkungen |
|
0 für n> 1 |
n/(n-2) für n> 2 |
0 |
(3n-6)/(n-4) für n > 4 |
0 |
0 |
|
Die t-Verteilung lässt sich mit Hilfe der Gammafunktion G darstellen:
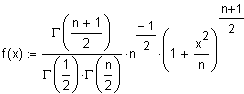
Für n=1 ergibt sich die Cauchy Verteilung.
G(1/2) = Wurzel(p)
n: Anzahl Freiheitsgrade
F: Verteilungsfunktion: nicht geschlossen darstellbar.
Für eine zusammenhängende Darstellung der Beziehungen Chi Quadrat Verteilung - t-Verteilung - F-Verteilung - Normalverteilung siehe hier.