Binomialverteilung Excel
Vertrauensbereich
Ohne Frames
Die Binomialverteilung beschreibt die
Situation "Ziehen mit Zurücklegen" oder "sehr grosse
Grundgesamtheit".
Verwandtschaftliche Beziehungen bestehen zu Normalverteilung,
Poissonverteilung und Hypergeometrischer
Verteilung.
Letztere beschreibt die Situation
"Ziehen ohne Zurücklegen" oder "sehr
kleine Grundgesamtheit".
zurück
zum Glossar
Binomialverteilung
Gegeben
sei eine Folge von n Bernoulli Experimenten mit den jeweils
möglichen Ausgängen a und b und den zugehörigen Wahrscheinlichkeiten p
und q, mit p+q=1.
Die
Binomialverteilung beantwortet die Frage, wie wahrscheinlich es ist,
dass mit den genannten Daten BIS ZU x Mal das Ereignis a eingetreten
ist.
Binomialverteilung
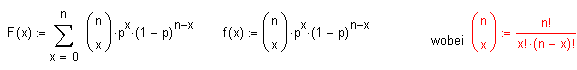 |
Beispiel: 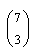 = =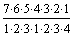 |
|
Zur einfachen Berechnung der Binomialkoeffizienten
(z.B.: 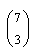 ) kann
das Pascal'sche Dreieck herangezogen
werden. ) kann
das Pascal'sche Dreieck herangezogen
werden.
Wenn p klein und n gross ist, kann man die
Binomialverteilung mit der Poissonverteilung
annähern.
Bei sehr grossen Zahlen n verwendet man
praktischerweise die Chernoff Ungleichung.
|
n:
Stichprobengrösse
p:
Anteil Merkmalsträger
in der Grundgesamtheit (0.....1)
F: Verteilungsfunktion
f:
Dichtefunktion
Praktische
Anwendung:
Weitere
Zahlenbeispiele siehe unter Chernoff Ungleichung.
Zur
graphischen Berechnung der Quantile der Binomialverteilung
siehe Larson Nomogramm, oder allgemein Nomogramm.
Graphisches
Hilfsmittel zur Bestimmung des Vertrauensbereiches
der relativen Häufigkeit P bei
Binomialverteilung siehe
Clopper-Pearson Nomogramm.
Die
Binomialverteilung kann als Grenzfall der Hypergeometrischen
Verteilung angesehen werden.
Die
Binomialverteilung gilt für den Fall unendlich grosser Grundgesamtheiten, denn bei unendlich
grossen Grundgesamtheiten ändert sich nämlich die relative
Zusammensetzung derselben aufgrund der bereits gezogenen Elemente
nicht.
(Deshalb das Zurücklegen der Kugeln in obigem Beispiel)
Siehe
auch Poissonverteilung: "Anzahl Fehler pro Einheit" und Kombinatorik.
Für
eine Veranschaulichung der Beziehungen
Hypergeometrische Verteilung - Binomialverteilung
- Poissonverteilung
- Normalverteilung
in Excelsiehe
hier.
Für
eine mathematische Beschreibung der zuvor genannten Beziehungen siehe
hier.
Für eine Exceldatei zur graphischen Berechnung von
Vertrauensintervallen unter Binomialverteilung siehe hier.
Zur
Herleitung von Mittelwert und Varianz der Binomialverteilung siehe
Vertiefung unter Charakteristische Funktion.
Für eine Auflistung der Wechselbeziehungen einiger
wichtiger Verteilungsfunktionen siehe
hier.
Für
die Bestimmung des "optimalen"
Parameters p einer
binomialverteilten Stichprobe siehe Beispiel unter Maximum Likelihood Estimation (MLE).
Anwendungsbeispiele aus der Zuverlässigkeitstechnik
1.
Vertrauensintervalle:
Unter
n = 38 geprüften Einheiten wurden k=2 defekte Einheiten gefunden.
Wie
gross ist das einseitige / zweiseitige 90% Vertrauensintervall für den
"wahren" (aber unbekannten) Auschussanteil?
=
Zwischen welchem maximalen (poben) und minimalen
(punten) Ausschussanteil bewegt sich der "wahre"
Ausschussanteil p mit der Wahrscheinlichkeit (1-a) = 10 % ?
Es
gilt (ohne weitere Herleitung) für die jeweils einseitigen
Vertrauensbereiche:
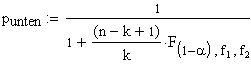 |
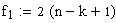
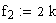
|
n: Anzahl geprüfter Einheiten
k:Anzahl defekter Einheiten
a: Wahrscheinlichkeit,
mit der der "wahre" Ausschussanteil unterhalb punten (bzw. je nach Fragestellung
oberhalb poben)
liegen soll.
|
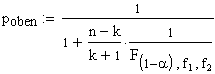 |
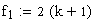
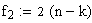
|
Für
den zweiseitigen Vertrauensbereich muss in beiden Formeln
lediglich F(1-a)durch F(1-a/2) ersetzt werden.
Der
Rest der Formeln sowie die Berechnung der Freiheitsgrade f1
und f2 bleiben gleich.
Für den einseitigen Bereich gilt jeweils
nur eine der obigen beiden Formeln, je nachdem, ob man den oberen oder
unteren Bereich meint. Für den zweiseitigen Bereich gelten natürlich
beide Formeln zusammen.
Die
Funktion F(a,f1,f2) kann man mit Excel
wie folgt berechnen:
FINV(a;f1;f2)
Ergebnis (einseitig):
poben = 13,4%
[mit FINV(0,1;6;72)]
punten =
1,4% [mit FINV(0,1;74;4)]
Der
Schätzwert liegt bei p = 2/38 = 5,3%
Für
hinreichend grosse n und k kann man mit der Normalverteilung annähern
und erhält das Vertrauensintervall auf viel einfachere Weise. Näheres
dazu
hier.
Anmerkung:
Obige
Formeln
sind eine von mehreren Möglichkeiten, die Vertrauensintervalle
für die
Binomialverteilung zu berechnen.
Weitere
Verfahren, auch Iterative, werden hier
beispielhaft gegenübergestellt.
2.Nochmal
Vertrauensintervalle:
Angenommen, es sind n Geräte im Feld. Die konstante
Ausfallrate dieser n Geräte sei l, die (konstante) Reparaturdauer
sei
R. Es werden ferner k Ersatzgeräte bereitgehalten.
Wie
gross ist die
Verfügbarkeit eines Ersatzgerätes
bei Ausfall eines Gerätes im Feld?
=
Wie gross ist die
Wahrscheinlichkeit, dass, wenn
ein Gerät im Feld ausgefallen ist, wenigstens ein Ersatzgerät
bereitsteht (also nicht alle vergriffen sind) ?
Die
Wahrscheinlichkeit berechnet sich zu
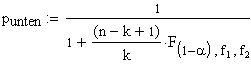 |
Zahlenbeispiel:
| n |
l |
R |
k |
| 2000 |
121,7/1.000.000
h |
4 h |
2 |
|
Hier
entspricht l dem l
in obiger Formel, und n*R entspricht dem t in obiger Formel. Die Frage
ist also, wie wahrscheinlich es ist, dass in n*R Betriebsstunden
höchstens 2 Ausfälle auftreten. |
| |
Ergebnis: F(2)=92,5% |
Bei
jedem Ausfall im Feld steht also mit 92,5% Wahrscheinlichkeit
mindestens 1 Ersatzeinheit bereit. |
3.
Operationscharakteristik
Siehe
hier
30.07.2006
zurück
zum Glossar
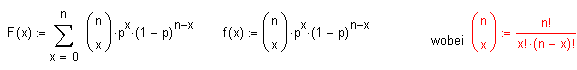
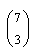 =
=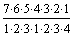
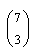 ) kann
das Pascal'sche Dreieck herangezogen
werden.
) kann
das Pascal'sche Dreieck herangezogen
werden.