Beispiel 1:

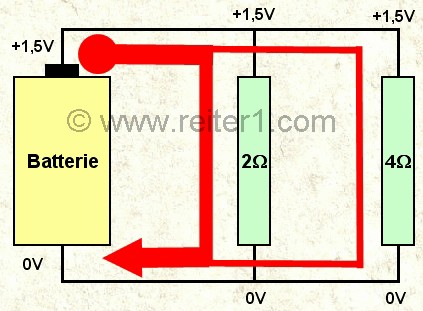
Zwei unterschiedliche Widerstände liegen parallel an einer 1,5V Batterie. Klemmt man einen davon ab, dann "sieht" der andere immer noch 1,5V und der durch ihn fliessende Strom ändert sich wegen I = U/R nicht.

Für den linken Widerstand gilt in Werten:

I_links =1,5V / 2Ω =0,75A, und für den rechten

I_rechts = 1,5V / 4Ω =0,375A.

Durch den 2Ω Widerstand fliesst also der doppelte Strom im Vergleich zum doppelt so grossen 4Ω Widerstand, was intuitiv einleuchtet und im Bild rechts durch die Dicke der roten Strompfeile wiedergegeben wird.

Würde man einen dritten Widerstand von z.B. 10Ω in Reihe dazuschalten, dann "sieht" auch dieser 1,5V und die Verhältnisse in ihm sind ebenfalls unabhängig vom Vorhandensein der anderen beiden Widerstände.

Für den 10Ω Widerstand würde ebenfalls gelten I = U/R, in Werten: I = 1,5V / 10W = 0,15A.

Wenn man alle Ströme zusammenzählt, so ergibt sich mit 3 parallelen Widerständen

I_gesamt = I₁ + I₂ + I₃ = U/R₁ + U/R₂ + U/R₃.

Da die Spannung U für alle 3 Widerstände gleich ist, kann man U auch ausklammern:

I_gesamt =  U x ( 1/R₁ + 1/R₂ + 1/R₃)

Wenn man sich in die Batterie hinein begibt und von den einzelnen Widerständen nichts weiss, dann würde man glauben, es sei nur ein einziger Widerstand angeschlossen, und zwar mit dem Wert R_gesamt = U / I_gesamt

Setzt man hier I_gesamt von weiter oben ein, so erhält man:

R_gesamt = U / {U x ( 1/R₁ + 1/R₂ + 1/R₃) }

=1 / (1/R₁ + 1/R₂ + 1/R₃)

Wenn man das etwas umstellt, dann sieht es eindrücklicher aus und ist leichter zu merken:

1/R_gesamt = 1/R₁ + 1/R₂ + 1/R₃

Mit dem Zahlenbeispiel von oben (2Ω, 4Ω und 10Ω) ergibt sich (das kleinste gemeinsame Vielfache von 2,4 und 10 ist 20):

1/R_gesamt = 1/2Ω + 1/4Ω + 1/10Ω = (10+5+2)/20Ω = 17/20Ω

Kehrwert bilden: R_gesamt = 20/17Ω ~ 1,176Ω.

In einer Parallelschaltung ist der Gesamtwiderstand immer kleiner als der kleinste Einzelwiderstand.

Weiter