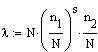,
wobei 
(Hinweis: In der Formel P = 1-elambda muss vor dem lambda ein Minuszeichen stehen)Im Gegensatz
zum Wald Wolfowitz Runs
Test, der die gesamte Wertereihe testet, wird
beim Iterationslängentest nur ein bestimmter Ausschnitt der Wertereihe
betrachtet.
zurück zum Glossar (Iterationslängentest)
Dieser Test addressiert die Begriffe "Glücks-" oder "Pechsträhne".
Voraussetzung: Dichotomes Merkmal.
Dieser Test ist derart rechenintensiv, dass im Rahmen dieses Glossars eigentlich gänzlich darauf verzichtet werden müsste.
Aufgrund der Bedeutung dieses Tests soll jedoch auf anschaulicher Ebene ausführlicher eingegangen werden.
Beispiel:
Eine Warteschlange mit 50
Personen. Die ersten 25 sind in der erstan Zeile, und die zweiten 25 in der 2. Zeile dargestellt.
| m | m | m | m | w | m | w | w | w | m | m | w | m | m | m | m | m | m | m | m | m | w | w | m | m |
| w | w | m | m | w | w | w | m | m | m | w | m | m | m | w | w | m | m | w | m | m | w | m | w | m |
Gesamt: 50 (N) m: 32 (n1) w:18 (n2) Serienlänge (s [n1]): 8 (rot hervorgehoben.
Es sind offensichtlich deutlich mehr Männer als Frauen in der Warteschlange.
Dennoch könnte man sich fragen, ob die "Achterserie" aus Männern (rot hervorgehoben) wirklich nur zufällig entstanden ist.
Vor dem Test muss man sich erst Folgendes klar machen:
| Fall
1 (schwieriger):
Man geht von einer gleichverteilten Geschlechterhäufigkeit aus (50%m, 50%w). Abstrahiert: Die Zusammensetzung der Grundgesamtheit ist bekannt. (Muss nicht unbedingt gleichverteilt sein) |
Fall
2 (einfacher):
Man nimmt den vorliegenden Datensatz als Grundgesamtheit (64%m, 36%w) Abstrahiert: Die Zusammensetzung der Grundgesamtheit ist unbekannt. Das vorliegende Datenmaterial wird als Grungesamtheit betrachtet. |
|
Man erhält für die theoretische Wahrscheinlichkeit der "Achterserie" (rot hervorgehoben) einen niedrigeren Wert .
Die Information "In der Reihe stehen an sich schon wesentlich mehr Männer als Frauen" wird nicht verwertet.
Dies entspricht der Situation, wo man nach der Wahrscheinlichkeit einer rein aus Männern bestehenden Achterserie fragt, bevor man die Reihe überhaupt je gesehen hat. |
Man erhält für die theoretische Wahrscheinlichkeit der "Achterserie" (rot hervorgehoben) einen höheren Wert .
Die Information "In der Reihe stehen an sich schon wesentlich mehr Männer als Frauen" wird in diesem Fall explizit verwertet.
Dies entspricht der Situation, wo man ausser der vorliegenden Reihe keinerlei weitere Information hat.
"Bedingter Test". |
Der Fall 1 ist deshalb schwieriger, da eben nicht genau von 50% m und 50% w ausgegangen wird, sondern von einer Verteilung, die im Mittel 50% m und 50% w ergibt.
Bei Fall 2 geht man degegen genau von z.B. 64% m und 36% w aus.
Berechnung der Überschreitungswahrscheinlichkeit des Auftretens mindestens einer Serie der Länge s
Zu Fall 2 (einfacher):
Die Serienlänge ist asymptotisch poissonverteilt, was intuitiv einleuchtet, da die Poissonverteilung die Verteilung der Anzahl Ereignisse pro Einheit beschreibt, in diesem Fall die Anzahl Serien einer bestimmten Länge pro Reihenlänge N.
2a) Asymptotische Berechnung
Ab N=30 kann man asymptotisch hinreichend genau rechnen.
Die
Überschreitungswahrscheinlichkeit ergibt sich zu ,
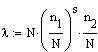wobei (Hinweis: In der Formel P = 1-elambda muss vor dem lambda ein Minuszeichen stehen)
und die Serie sich auf n1 bezieht.
Dies folgt unmittelbar aus der Poissonverteilung (F: Verteilungsfunktion, f: Dichtefunktion)
 |
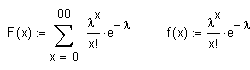Würde man nach der Wahrscheinlichkeit für genau x = 0 Iterationen fragen, hätte man F(0) = e-l . Die Wahrscheinlichkeit für mindestens 1 Iteration ist demnach 1- e-l. |
l ist der Erwartungswert der poissonverteilten Serienlänge.
In dem Beispiel ergibt sich mit N=50, n1= 32, n2=18, s= 8:
=0.507 =>
P=39.8% (Hinweis: die 16 links in der Formel muss 18 sein)
Man würde also mit fast 40% Wahrscheinlichkeit eine Achterserie aus Männern in einer Warteschlange erwarten, die aus 32 Männern und 18 Frauen besteht.
2b) Exakte Berechnung
Ohne weitere Herleitung:
Die Überschreitungswahrscheinlichkeit ergibt sich zu
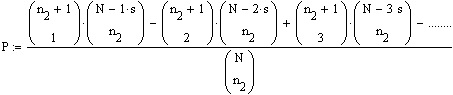
In dem Beispiel ergibt sich mit N=50, n1= 32, n2=18, s= 8:
=
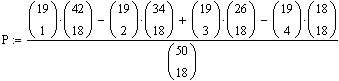35.1%
Dieser Wert ist etwas kleiner als der durch den asymptotischen Test ermittelte Wert.
Der asymptotische Test rechnet also Konservativ.
Zu Fall 1 (schwieriger):
Dieser Test übertrifft den Aufwand des Falls 1 noch erheblich und erfordert einigen Programmieraufwand.
Deshalb sei hier gänzlich auf Formeln verzichtet und gleich auf die von Cochran entwickelte Tafel verwiesen:
 |
|
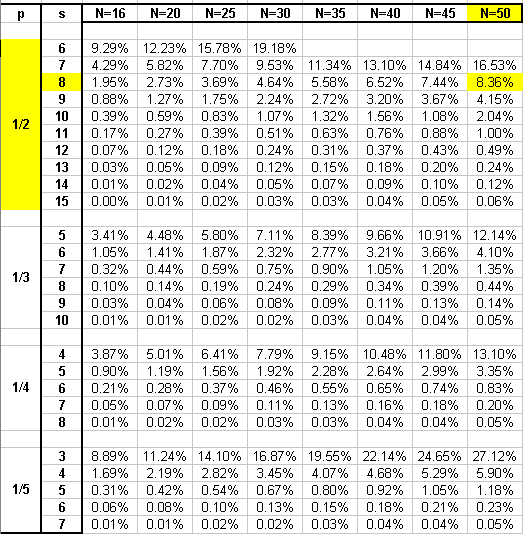p: Einzelwahrscheinlichkeit derjenigen Ereignisse, die die zu untersuchende Serie bilden. s: Länge dieser Serie N: Gesamtlänge der Reihe, die die zu untersuchende Serie enthält.
Im Beispiel sind: N=50, s=8 und p = 1/2 Aus der Tafel links liest man dafür eine Überschreitungswahrscheinlichkeit von 8.36% ab. Bei Gleichverteilung der Geschlechter käme in einer Warteschlange aus 50 Personen eine Achterserie, bestehend aus Männern, nur mit einer Wahrscheinlichkeit von ca. 8% zustande. |
zurück zum Glossar (Iterationslängentest)
25.08.2005