Zur Hauptseite  ..\

zur Glossarseite    Ohne Frames

 

Faktorenanalyse Hauptkomponentenanalyse Principal Components Analysis PCA 

 

 

Daten in einem höherdimensionalen Raum sollen in wenigen Dimensionen möglichst getreu reproduziert werden. 

Metrisches Skalenniveau.

Datenreduktionsverfahren, um Zusammenhänge überschaubarer zu machen. 

Strukturen-entdeckendes Verfahren.

Zur Kategorie der Explorativen Datenanalyse gehörendes Verfahren. 

Bei der Faktorenanalyse werden im Gegensatz zur Clusteranalyse die Merkmale oder Variablen gruppiert, nicht die Fälle, Individuen oder Objekte. 

Hier wird also die Dimensionalität des Datenmaterials verkleinert: "Finde diejenigen (wenigen) Linearkombinationen der Variablengesamtheit, die einen Grossteil der Varianz erklären".

Möglichst wenige Linearkombinationen (=Faktoren) von Merkmalen der Objekte werden gebildet, und zwar derart, dass 

Einen Faktor kann man sich (analog zu einer Regressionsgeraden) als besten Repräsentanten einer Gruppe von Variablen vorstellen, wobei eine Variable in mehreren Faktoren enthalten sein kann ("Variablenbüschel", Linearkombination). 

Die Faktorenanalyse beantwortet somit die Frage, ob es eine deutlich geringere Anzahl von künstlichen Variablen (=Faktoren) gibt, die die Zusammenhänge zwischen allen Untersuchungsvariablen weitgehend zu erklären in der Lage sind.

 

Jeder gefundene Faktor reduziert die Dimensionalität des verbleibenden Datenmaterials jeweils um 1. 

Bildet man so viele Faktoren, wie das ursprüngliche Datenmaterial Variablen besitzt dann würde das Faktorenmodell 100% der Streuung der Daten erklären. 

Daraus wäre aber nichts gewonnen; wichtig ist, dass man nur die ersten paar wenigen Faktoren berücksichtigt, die idealerweise den Grossteil des Datenmaterials erklären. 

 

Anwendungsbereiche sind grundsätzlich die selben wie bei der Clusteranalyse, tendenziell jedoch eher in wissenschaftlichen Bereichen, da bei dieser Methode künstliche ( latente) Variablen (Faktoren) geschaffen werden, die nicht immer einfach zu interpretieren sind. 

 

Veranschaulichungen

 

Auch die Hauptkomponentenanalyse "lebt" davon, die Varianz eines Datensatzes mit möglichst geringem Modellaufwand möglichst vollständig abzubilden. 

Auch hier liegt die Annahme zugrunde, dass grosse Varianz = grosser Informationsgehalt bedeutet.

 

a) Wie kann man sich eine optimale Reduzierung der Dimensionalität vorstellen? 

 

Damit Faktorenanalyse vernünftige Ergebnisse herausbringt, muss das Datenmaterial eine wie auch immer geartete Struktur oder Auffälligkeiten vorweisen. 

Nehmen wir einmal an, wir wüssten, dass unser aus 5 Dimensionen bestehender Datensatz eine 4-dimensionale Zigarre im 5-dimensionalen Raum darstellt. 

Eine Hauptkomponentenanalyse würde als erste Hauptkomponente die Längsachse der Zigarre detektieren. 

Angenommen, in dem verbleibenden 4-dimensionalen Raum würde die Anordnung der Datenpunkte nun einen flachen Teller ergeben, dann würden die 2. und 3. Hauptkomponente in der Ebene des Tellers liegen, und zwar senkrecht zueinander. 

Weiterhin angenommen, in dem nun verbleibenden 2-dimensionalen Raum wäre keine besondere Struktur mehr erkennbar, dann würden die 4. und 5. Hauptkomponente zwar den verbleibenden Rest der Daten erklären; deren Beitrag wäre aber ausserordentlich gering, sodass das in diesem Anschauungsbeispiel gefundene "optimale" Modell nur aus 3 Faktoren bestehen würde.

Das gefundene Modell wäre demnach 3-dimensional, wobei in diesen 3 neu ausgerichteten Dimensionen der grösste Teil der Information aller 5 ursprünglichen Dimensionen enthalten ist. 

 

b)  Was passiert im Bezug auf die Varianz? 

 

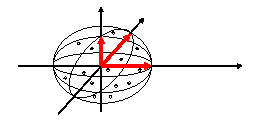
Bei der Suche nach der ersten Hauptkomponente wird das n-dimensionale Koordinatensystem derart gedreht, dass eine Achse in diejenige Richtung zeigt, in der die Datenpunkte am weitesten streuen = die grösste Varianz besitzen = am meisten Information beinhalten. 

Diese Achse wird ab nun fixiert und stellt die erste Hauptkomponente dar. 

Nun wird bei festgehaltener erster Achse das aus den restlichen Achsen bestehende System derart gedreht, dass wieder eine Achse in diejenige Richtung zeigt, in der die Datenpunkte in dem nun verbleibenden Datenraum die grösste Varianz besitzen, usw. 

 

c) Einige Begriffe rund um Faktoranalyse

 

Begriff Erklärung Beispielskizze: Aus einem 5-dimensionalen Datensatz (Variablen A,B,C,D,E) wurden 3 Faktoren (J,K,L) bestimmt ("extrahiert")
Eigenvektor = Faktor
Faktorladung 

= Korrelationskoeffizient zwischen einer Variablen und einem Faktor.

Idealerweise laden alle Variablen nur auf einem Faktor hoch, = jede Variable wäre in nur einem Faktor enthalten. 

Tabelle mit Korrelationskoeffizienten
Variable/Faktor J K L
A 0.5 0.6 0.2
B 0.8 0.4 0.2
C 0.6 0.3 0.3
D 0.4 0.4 0.3
E 0.3 0.2 0.1
Beispiel: Die Faktorladung der Variablen A auf den Faktor J beträgt 0.5.
Eigenwert

Masszahl für den Erklärungsanteil eines Faktors im Hinblick auf die Varianz aller Variablen.

= der Summe der quadrierten Faktorladungen eines Faktors. 

Die Eigenwerte der in das Modell übernommenen Eigenvektoren sollten "deutlich" grösser sein als die Eigenwerte der nicht in das Modell übernommenen Faktoren 

Siehe obige Tabelle: Der Eigenwert des Faktors K beträgt (0.6)2 + (0.4)2 + (0.3)2 + (0.4)2 + (0.2)2 = 0.81. 

 

Entsprechend erhält man für J = 1.5, und für L = 0.27
Kommunalität  Teil der Gesamtvarianz einer (Ausgangs-) Variablen, die durch alle gebildeten Faktoren erklärt wird. Idealerweise findet sich jede Ausgangsvariable in dem Satz neu gebildeter Faktoren vollständig wieder. Beispiel: 

Die Varianz (= der Informationsgehalt) der Variablen A ist zu 35% in Faktor J, zu 33% in K und zu 10% in L enthalten. 

Damit ergibt sich die Kommunalität von A zu (35+33+10)% =  78% 

Wenn sich weitere10% der Varianz von A in K, und weitere 5% in L wieder finden, dann erklärt das aus 3 Faktoren bestehende Modell die Variable A zu (78+10+5)% = 93%.
Scree Plot Paretoartige graphische Darstellung der nach der Grösse sortierten Eigenwerte. Dient als "augenscheinliches" Entscheidungskriterium für die Rechtfertigung derjenigen gefundenen Faktoren, die man in das Modell einbezieht. 

Die Eigenwerte von J, K und L lauten 1.5,   0.81,   und 0.27. 

Die Eigenwerte zweier weiterer Faktoren seien 0.22 und 0.13. 

Damit ergibt sich folgender Scree-Plot:

Dem Plot entnimmt man visuell, dass bereits der Faktor L eher dem "Rauschen" zuzuordnen ist, und man das Modell auf 2 Faktoren beschränken sollte.

 

Faktoranalyse auf höchstens ordinalem Skalenniveau heisst Korrespondenzanalyse. 

Siehe auch Partial Least Squares Regression.

 

Datenschutzhinweise