Sequentieller Binomialtest

Beispiel für sequentielles Testen

Zurück zum sequentiellen Binomialtest

Binomialtest, sequentieller 

 Dieses Kapitel besteht aus folgenden Unterkapiteln. 

Bei einem sequentiellen Test wird gerade so lange getestet, bis genug Evidenz für eine statistische Entscheidung vorhanden ist. 

Der Test wird also genau dann abgebrochen, wenn zum ersten Mal eine eindeutige Entscheidung getroffen werden kann.

Deshalb müssen Nullhypothese, Alternativhypothese und Effektgrösse explizit formuliert werden.

 (Siehe dazu Anmerkungen zu statistischen Hypothesen, a) und b)) 

1.) Einseitiger sequentieller Binomialtest: Testen des Anteilsparameters EINER Population

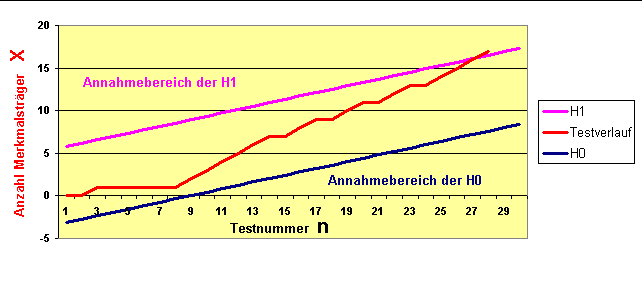
Zur Erklärung der Funktionsweise des sequentiellen Binomialtests nehmen wir aus didaktischen Gründen das graphische Ergebnis vorweg;

der Rechenweg folgt weiter unten:

Man beginnt im Koordinatenursprung (n=0 und x=0).

Mit jedem durchgeführten Test geht man auf der horizontalen Achse einen Schritt nach rechts. War der Test positiv, geht man gleichzeitig einen Schritt nach oben. 

Somit ergibt sich eine "Testspur", welche im obigen Bild beispielhaft durch die rote Linie dargestellt ist. 

In diesem Beispiel durchquert die Testspur nach dem 28 ten Test die H1 Linie. 

Das bedeutet, dass nach 28 Testindividuen genügend Daten für die Annahme der vor dem Test formulierten Alternativhypothese, H1, vorhanden waren.

Der Test konnte also nach dem 28. Testindividuum mit klarem Ergebnis abgebrochen werden.

Herleitung der Funktionsweise des einseitigen Binomialtests:

Berechnung der beiden Geraden H0 und H1. 

1.) Formulierung der beiden Hypothesen, Bestimmung der Effektgrösse. 

H0: "Der Anteilswert roter Kugeln in der Urne betrage p₀ = 0,3". 

H1: "Der Anteilswert roter Kugeln in der Urne betrage p₁= 0,5". 

Der zu entwickelnde sequentielle Binomialtest soll also messen, ob der tatsächliche Anteilswert eher 0,3 oder 0,5 beträgt. Die Differenz zwischen 0,3 und 0,5, die sogenannte Effektgrösse,  wird für bedeutsam erachtet. 

2.) Berechnung der beiden Geraden. 

2a) Vorbemerkungen

Wir betrachten nun eine laufende Testserie aus bisher n erfolgten Durchgängen, wobei x mal das gesuchte Merkmal beobachtet worden ist.

(Man hat z.B. 15 Durchgänge durchgeführt, 6 davon waren "positiv". Siehe dazu Binomialverteilung)

Wenn die Nullhypothese gilt, also in Wahrheit  p = p₀ ist, dann ist die Wahrscheinlichkeit, in n Durchgängen genau x "Positive" zu finden 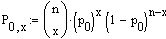   Dies entspricht der Situation A: in obiger Tabelle.

Wenn jedoch die Alternativhypothese gilt, also in Wahrheit p=p₁ ist, dann ist die Wahrscheinlichkeit, in n Durchgängen genau x "Positive" zu finden 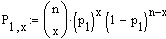   Dies entspricht der Situation B: in obiger Tabelle.

Nun kann man wegen Normierungsproblemen zwar nicht direkt fordern, dass P_0,x grösser als(1-Alpha Risiko) und P_1,x kleiner als Beta Risiko sein soll, aber der Quotient (siehe A: und B: in obiger Tabelle) 

muss gleich oder  grösser sein, als der Quotient aus den beiden zuvor genannten Wahrscheinlichkeiten  

(P_0,x / P_1,x), damit der Test sinnvoll entscheidet.  Für den Grenzfall "=" ergibt sich

-->  

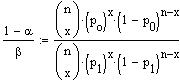
Nach Herauskürzen von (n über x), Logarithmieren beider Seiten und Auflösen nach x erhält man  

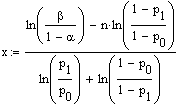
Dies ist eine Geradengleichung der Form x = a*n +b₀,

mit 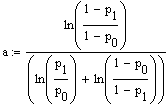  und   .

n, also die Anzahl bereits erfolgter Durchgängen ist dabei die Unabhängige Variable, x ist die Abhängige Variable. Diese Geradengleichung gibt zum Zeitpunkt "bereits n Durchgänge durchgeführt"  die Höchstanzahl x "positiver" Testergebnisse an, damit die Nullhypothese (nach genau n Durchgängen) noch angenommen werden kann.  

Mit völlig analogen Überlegungen erhält man für die Geradengleichung x = a*n +b₁ zum Zeitpunkt "bereits n Durchgänge durchgeführt" für die Mindestanzahl x "positiver" Testergebnisse, damit die Alternativhypothese (nach genau n Durchgängen) angenommen werden kann: 

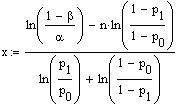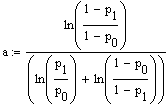  ,  mit   und

Es ist leicht zu erkennen, dass die beiden Geraden parallel zueinander sind (Steigung = a). 

Da man schon bei der graphischen Methode ist, lässt sich gleich die Frage: 

3.) Erwartungswert der Anzahl Durchgänge bei gegebenen p₀ und p₁,  

anschaulich beantworten.  

Dazu wird im Folgenden nochmal das obige Bild dargestellt.

Es ist leicht einsichtig, dass die Steigung einer völlig geraden (fiktiven) Testspur (entspricht roter Linie) im Mittel gleich dem "wahren" (aber unbekannten) Anteilswert p ist. 

Zieht man also durch den Nullpunkt des Koordinatensystems eine Gerade mit der Steigung p, dann ist die Abszisse (Wert auf der horizontalen n-Achse) des Schnittpunkts dieser Geraden mit einer der beiden Geraden H0 oder H1 offenbar der Erwartungswert der Anzahl durchzuführender Tests. 

Für den Fall, dass die Steigung p ähnlich der Steigung der Geraden H0 und H1 ist,  gilt diese Betrachtungsweise nicht, da der Schnittpunkt mit einer der beiden Geraden H0 und H1 sehr weit links zu liegen käme. In diesem Fall wäre es wahrscheinlicher, dass die Testspur rein zufällig bereits früher eine der beiden Geraden schneidet.  

Für eine Excel Beispieldatei des einseitigen sequentiellen Binomialtests siehe hier. 

Abgesehen von der graphischen Abschätzung der zu erwartenden Anzahl Tests gibt es noch eine algebraische Abschätzung in parametrisierter Form.

Diese wird im folgenden Unterabschnitt, Operationscharakteristik, kurz dargelegt.

4.) Operationscharakteristik des einseitigen sequentiellen Binomialtests.

Die Operationscharakteristik Oc(p) gibt die Annahmewahrscheinlichkeit der Nullhypothese in Abhängigkeit des "wahren" (aber unbekannten) Anteilswertes p an.

Im Falle des sequentiellen Binomialtests lässt sich die Operationscharakteristik nicht in geschlossener Form angeben. Es existiert aber eine parametrische Form, welche im Folgenden ohne Herleitung lediglich angegeben wird.

Für beliebige Werte von z ergeben sich Wertepaare (p|Oc(p)) wie folgt: 

,    

Im obigen Beispiel (p₀=0,3,  p₁=0,5, a=1%,  b=5%) erhält man nach Durchrechnen mit verschiedenen z folgende graphische Darstellung der Operationscharakteristik.

Der Graphik kann man direkt entnehmen:

Wenn der "wahre" Anteilswert p bei p₀=0,3 liegt (grüner Pfeil), dann beträgt die Annahmewahrscheinlichkeit der Nullhypothese 99%

Wenn der "wahre" Anteilswert p bei p₁=0,5 liegt (roter Pfeil), dann beträgt die Annahmewahrscheinlichkeit der Nullhypothese 5%

(Diese Werte entsprechen logischerweise dem kurz zuvor festgelegten Alpha- bzw. Betarisiko)

Für eine Excel Beispieldatei der Operationscharakteristik des einseitigen sequentiellen Binomialtests siehe hier. 

Den Erwartungswert E(n)der benötigten Anzahl Tests bis zur Entscheidung kann man wie folgt berechnen:

, für p ungleich a,                       , für p = a.

,   ,

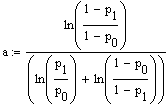Anmerkung des Verfassers: Die beiden für E(n) angegebenen Formeln (also für p = a bzw. für p ungleich a) überlappen sich bei Weitem nicht. Die erste Formel für E(n) a nimmt "in der Gegend von a" extrem viel höhere Werte an als die zweite Formel für E(n). Dies ist graphisch auch verständlich, da der Schnittpunkt der H1-Geraden und der (idealerweise geraden) Testspur extrem weit rechts zu liegen kommt. In der nächsten Umgebung von a, wo die erste Formel höhere Werte als die zweite liefert, ist  stets der (niedrigere) Wert der zweiten Formel zu nehmen.

Zurück zum sequentiellen Binomialtest                      Nach oben

2.) Einseitiger sequentieller Binomialtest: Vergleich der Anteilsparameters ZWEIER Populationen.

Dieser Test unterscheidet sich rechnerisch vom Testen EINES Anteilsparameters lediglich in der Bestimmung der Wahrscheinlichkeiten zu Beginn des Tests.

Während sich beim einseitigen sequentiellen Binomialtest (Testen des Anteilswertes EINER Population) die Wahrscheinlichkeiten direkt formulieren lassen,

müssen diese beim Vergleich der Anteilswerte ZWEIER Populationen erst berechnet werden.

Prinzipieller Ablauf eines Testschrittes:

In jedem Testschritt werden 2 Testindividuen gewählt. Führe an einem Individuum die Behandlung A, am Anderen die Behandlung B durch.

Vergleiche die Ergebnisse der Individuen nach der Behandlung.

Es sind 4 Möglichkeiten denkbar:  (++), (+-), (-+), (--). 

Endet ein Testschritt mit der Möglichkeit (++) oder (--), dann wird dieser Testschritt nicht gewertet. 

Angenommen, die Erfolgswahrscheinlichkeiten für Methode A und B seien p_a und p_b.

Bei Gültigkeit der Nullhypothese H0 ist unmittelbar einleuchtend, dass unabhängig von p_a (=p_b) die Kombinationen (+-) und (-+) gleichwahrscheinlich auftreten werden, und zwar mit jeweils 0,25. (Die Kombinationen (++) und (--) werden ebenfalls mit einer Wahrscheinlichkeit von 0,25 auftreten. 

Gilt die Alternativhypothese, dann wird (+-) mit der Wahrscheinlichkeit , und (-+) mit der Wahrscheinlichkeit auftreten.

Beide zusammen ergeben aber nicht 1, sondern weniger. Dies ist an sich nicht schlimm; da man aber die Kombinationen (++) und (--) beim Testdurchlauf nicht verwertet, muss man P_a und P_b so skalieren, dass sie zusammen 1 ergeben.

Somit ergeben sich nach Skalierung , und als diejenigen Wahrscheinlichkeiten,

 mit denen man den im vorigen Kapitel 1.) beschriebenen einseitigen sequentiellen Binomialtest durchführt. 

Anmerkung:

Die im Abschnitt 1.) dieses Kapitels beschriebenen Ausführungen zur Operationscharakteristik und zum Erwartungswert für die mittlere Anzahl bis zur Entscheidung notwendiger Durchgänge lassen alle Durchgänge unberücksichtigt, deren Ausgang entweder (++) oder (--) ist.

Die tatsächlich durchzuführende mittlere Anzahl Durchgänge kann also bedeutend höher liegen.

Dies lässt sich aber durch Berücksichtigung der Wahrscheinlichkeiten vor der Skalierung auf 1 einfach berechnen.

Zurück zum sequentiellen Binomialtest                      Nach oben

3.) Zweiseitiger sequentieller Binomialtest: Testen des Anteilsparameters EINER Population

Der einzige Unterschied zum einseitigen sequentiellen Binomialtest besteht darin, dass die Alternativhypothese in 2 Richtungen formuliert wird. 

Auch hier sei das graphische Ergebnis aus didaktischen Gründen vorweggenommen:

Man beginnt im Koordinatenursprung (n=0 und x=0).

Mit jedem durchgeführten Test geht man auf der horizontalen Achse einen Schritt nach rechts.

War der Test positiv, geht man einen Schritt nach oben, war er negativ, geht man einen Schritt nach unten. 

Somit ergibt sich eine "Testspur", welche im obigen Bild beispielhaft durch die rote Linie dargestellt ist. 

In diesem Beispiel durchquert die Testspur nach dem 15 ten Test die obere H1 Linie. 

Das bedeutet, dass nach 15 Testindividuen genügend Daten für die Annahme der vor dem Test formulierten Alternativhypothese, H1 vorhanden waren.

Der Test konnte also nach dem 15. Testindividuum mit klarem Ergebnis abgebrochen werden.

Der zweiseitige sequentielle Binomialtest ist leider beschränkt im Hinblick auf:

• Nullhypothese: p₀ = 0,5 (andere Werte als 0,5 sind nicht erlaubt)

• Alternativhypothese:  p_1oben und p_1unten müssen spiegelbildlich zu 0,5 liegen.

In diesem Beispiel ist p₀ = 0,5,      p_1oben = 0,8,     p_1unten= 0,2

Die Hypothesenformulierung lautet hier also z.B.:

H0: "Der Anteilswert roter Kugeln in der Urne betrage p₀ = 0,5". 

H1: "Der Anteilswert roter Kugeln in der Urne betrage p₁= 0,8 oder 0,2". 

Der zu entwickelnde sequentielle Binomialtest soll also messen, ob der tatsächliche Anteilswert eher 0,5 oder 0,8 bzw 0,2 beträgt.

Die Differenz zwischen 0,5 und 0,8, Effektgrösse,  wird durch die Formulierungen als bedeutsam beurteilt. 

Die 4 Geradengleichungen erhält man aufgrund ähnlicher Betrachtungen wie im einseitigen sequentiellen Binomialtest.

3.) Erwartungswert der Anzahl Tests bei gegebenen p₀ und p₁. 

Auch im zweiseitigen Fall ist einsichtig, dass die Steigung einer geraden, fiktiven Testspur (entspricht roter Linie) im Mittel gleich dem "wahren" (aber unbekannten) Anteilswert p ist. 

Zieht man also durch den Nullpunkt des Koordinatensystems eine Gerade mit der Steigung p, dann ist die Abszisse (Wert auf der horizontalen Achse) des Schnittpunkts dieser Geraden mit einer der 4 Geraden H0 oder H1offenbar der Erwartungswert der Anzahl durchzuführender Tests. 

Für den Fall, dass die Steigung p im Bereich der Steigung der Geraden H0 und H1 ist,  gilt diese Betrachtungsweise natürlich nicht.  

Für eine Excel Beispieldatei des zweiseitigen sequentiellen Binomialtests siehe hier. 

Zurück zum sequentiellen Binomialtest                      Nach oben

4.) Zweiseitiger sequentieller Binomialtest: Vergleich der Anteilsparameter ZWEIER Populationen   

Dieser Test unterscheidet sich rechnerisch vom Testen EINES Anteilsparameters lediglich in der Bestimmung der Wahrscheinlichkeiten zu Beginn des Tests.

Während sich beim einseitigen sequentiellen Binomialtest (Testen des Anteilswertes EINER Population) die Wahrscheinlichkeiten direkt formulieren lassen,

müssen diese beim Vergleich der Anteilswerte ZWEIER Populationen erst berechnet werden. 

Völlig analog ergeben sich die beiden zu 1 skalierten Wahrscheinlichkeiten für die Kombinationen (+-) und (-+) zu

und .

Mit diesen beiden ermittelten Wahrscheinlichkeiten bestreitet man nun den zweiseitigen sequentiellen Binomialtest genau so, wie er im Abschnitt 3.) dieses Kapitels beschrieben ist.

Zurück zum sequentiellen Binomialtest                      Nach oben

5.) Sequentielle Varianten diverser  weiterer Tests

Im Folgenden werden die sequentiellen Varianten einiger Tests erläutert.

Diese Tests haben gemeinsam, dass sie binomialverteilungsbasiert sind und man sie deshalb in eine Form des sequentiellen Binomialtests bringen kann.

5a) Sequentieller Vorzeichentest.

Beim Vorzeichentest wird für jedes Wertepaar überprüft, ob der erste oder der zweite Wert grösser ist.

Bei Wertegleichheit bleibt das betreffende Wertepaar unberücksichtigt.

Unter der Nullhypothese H0 beträgt die Wahrscheinlichkeit p dafür, dass der erste Wert eines Paares grösser als der zweite Wert ist, = 0,5.

Der sequentielle Vorzeichentest in der

• einseitigen Form funktioniert also wie der in Abschnitt 1.) dieses Kapitels beschriebene

  einseitiger sequentieller Binomialtest: Testen des Anteilsparameters EINER Population,

  bei dem für p₀ = 0,5 und für p₁ ein von 0,5 verschiedener Wert genommen wird.

• zweiseitigen Form funktioniert entsprechend wie der in Abschnitt 3.) dieses Kapitels beschriebene

  zweiseitiger sequentieller Binomialtest: Testen des Anteilsparameters EINER Population,

  bei dem für p₀ = 0,5 und für p_1oben  und p_1unten jeweils zu 0,5 spiegelbildliche Werte genommen werden.

5b) Sequentieller McNemar Test

Beim McNemar Test bestehen die Wertepaare aus je einem Wert vor- und nach einer "Behandlung".

Der sequentielle Charakter dieses Tests ergibt sich folgendermassen:

.......

Teste Individuum n vor, dann nach der Behandlung.

Prüfe auf Signifikanz.

Teste Individuum n+1 vor, dann nach der Behandlung.

Prüfe auf Signifikanz.

.......

bis zur Entscheidung.

Von den nach jedem Testschritt denkbaren 4 Möglichkeiten (++), (+-), (-+), (--) bleiben (++) und (--) unberücksichtigt.

(Der McNemar Test ist ja ein Vierfelder Test, bei dem nur 2 der 4 Felder interessieren)

Der sequentielle McNemar Test in der

• einseitigen Form funktioniert also wie der in Abschnitt 2.) dieses Kapitels beschriebene

  einseitiger sequentielle Binomialtest: Vergleich der Anteilsparameter ZWEIER Populationen,

  bei dem für p₀ = 0,5 und für p₁ ein von 0,5 verschiedener Wert genommen wird.

• zweiseitigen Form funktioniert entsprechend wie der in Abschnitt 3.) dieses Kapitels beschriebene

  zweiseitiger sequentieller Binomialtest: Vergleich der Anteilsparameter ZWEIER Populationen,

  bei dem für p₀ = 0,5 und für p_1oben  und p_1unten jeweils zu 0,5 spiegelbildliche Werte genommen werden.

5c) Sequentieller Vierfelder Test.

Der sequentielle Vierfelder Test entspricht formal ganz und gar dem zuvor beschriebenen sequentiellen McNemar Test.

Allerdings werden hier die Kombinationen (++) und (--) mit berücksichtigt.

Zurück zum sequentiellen Binomialtest                      Nach oben

20.08.2005

Datenschutzhinweise